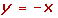Grafique las siguientes funciones:
PORTAFOLIO DE GLORIA
ACTIVIDADES DE CÁLCULO I, ÚTILES PARA EL DESARROLLO Y COMPRENSIÓN DE ALGUNOS TEMAS
Buscar este blog
lunes, 9 de mayo de 2011
sábado, 9 de abril de 2011
Actividad 2
Cónicas: La Hipérbola
HIPÉRBOLA
Es el lugar geométrico del conjunto de puntos P(X,Y) del plano cuya diferencia de distancias a dos puntos fijos (focos) es constante.
Esa constante (k) es igual a 2a y no es más que la distancia entre los dos vértices de la hipérbola.
| d(P,F1) - d(P,F2) |=2a
ELEMENTOS DE LA HIPÉRBOLA
Focos: Son dos puntos fijos (F y F') y respecto a ellos, la diferencia de distancias permanecen constante (en valor absoluto) a cualquier punto de dicha hipérbola.
El centro (O): es el punto medio de los focos.
Eje focal: Es la recta que pasa por los focos.
Eje secundario o imaginario: Es la mediatriz (perpendicular al punto medio) del segmento 
Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.
Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'.
Distancia focal: Es el segmento  de longitud 2c, es decir, OF = OF' = c
de longitud 2c, es decir, OF = OF' = c
Eje mayor: Es el segmento  de longitud 2a.
de longitud 2a.
Eje menor: Es el segmento  de longitud 2b.
de longitud 2b.
Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
Asíntotas: son las tangentes a la curva en el infinito. Los ejes son bisectrices de las asíntotas y de ecuaciones:

La excentricidad: mide la abertura mayor o menor de las ramas de la hipérbola
Ecuación de una Hipérbola
La ecuación de la hipérbola será:
Si el eje focal de la hipérbola es horizontal entonces, centro está en  , los vértices están en
, los vértices están en  y los focos están en
y los focos están en  .
.
La ecuación de la hipérbola será:
Si el eje focal de la hipérbola es vertical entonces, el centro está en  , los vértices están en
, los vértices están en  , los focos están en
, los focos están en  .
.
Ecuación Reducida: Es la ecuación de la hipérbola cuyos ejes coinciden con los ejes coordenadas, y, por tanto, el centro de hipérbola con el origen de coordenadas.
Los focos son F'(−c, 0) y F(c, 0)
Cuando los focos están sobre el eje Y, los focos son F'(0, −c) y F (0, c).
La ecuación es:
NOTA: Las hipérbolas en las que los semiejes son iguales se llaman equiláteras, por tanto a = b. Y su ecuación es:
COMO PASAR DE ECUACIÓN GENERAL A CANÓNICA
OJO: A y B tienen signos opuestos
Ejemplo Tipo:
1.- Hallar la ecuación canónica, los focos y los vértices de la hipérbola cuya ecuación es:
Datos:
Ecuación de la hipérbola: 
Fórmulas o conceptos:
Focos
Vértices
Resolución:
Completando el cuadrado en ambas variables
Por lo tanto, el centro está en  , y es vertical
, y es vertical
Los vértices están en V(2,0) V(2,-6)
COMO PASAR DE ECUACIÓN CANÓNICA A GENERAL
OJO: A y B tienen signos opuestos
Ejemplo Tipo:
2.- Pasar a la forma general, la ecuación canónica  , .
, .
Datos:
Ec. canónica: 
Conceptos: Cónicas e hipérbola, mínimo común multiplo, productos notables y Ecuaciones.
Desarrollo:
Es una hiperbola porq (x-2)2-(y+3)2tienen signos diferentes.
4(x-2)2-9(y+3)2=36
4(x2-4x+4)-9(y2+6y+9)=36
4x2-16x+16-9y2-54y-81=36
4x2-9y2-16x-54y-101=0
SOLUCION:
La ecuación de la forma general queda:
4x2-9y2-16x-54y-101=0
3.- Determinar una ecuación de la hipérbola que pasa por el punto de coordenadas (2,8), si uno de sus vértices está en V (0-4), su centro coincide con el origen del sistema de coordenadas y su eje focal es perpendicular al eje de las abscisas.
Datos:
V(0,-4) Vértice
C(0,0) Centro en el origen del sistema de coordenadas
P(2,8) Punto por el que pasa la hipérbola
El eje focal es perpendicular al eje de las abscisas, eje X
La ecuación es de la forma:
Conceptos:
Cónicas, vértices, centro, caracteristicas de la hipérbola
Resolución:
Encontramos a por la distancia del vértice al centro, por lo tanto:
a=4
Como tenemos el punto P(2,8), sabemos que hipérbola pasa por ese punto, y que a=4, sustituimos x, y, a en la ecuación y encontramos b2:
a2=16
conociendo los cuadrados de a y de b, sustituimos en la ecuación:
SOLUCION:
La ecuación de la hipérbola queda:
Y de la forma general queda:
3y2-48x2-64=0
Suscribirse a:
Comentarios (Atom)